AbstractThe global mean surface temperature (GMST) is a key metric for monitoring climate change. A current debate revolves around whether there has been a noticeable increase in the warming rate since the 1970s. This study aims to determine if such an acceleration is statistically detectable. We employ changepoint models—statistical methods tailored for identifying structural changes in time series—to analyze four GMST records from 1850 to 2023. Our findings provide limited support for a warming surge; in most temperature time series, no change in the warming rate after the 1970s is observed, despite the record-breaking temperatures recorded in 2023. Consequently, we estimate that at least a 55% increase in the warming trend would be necessary for a surge to be statistically detectable at present.
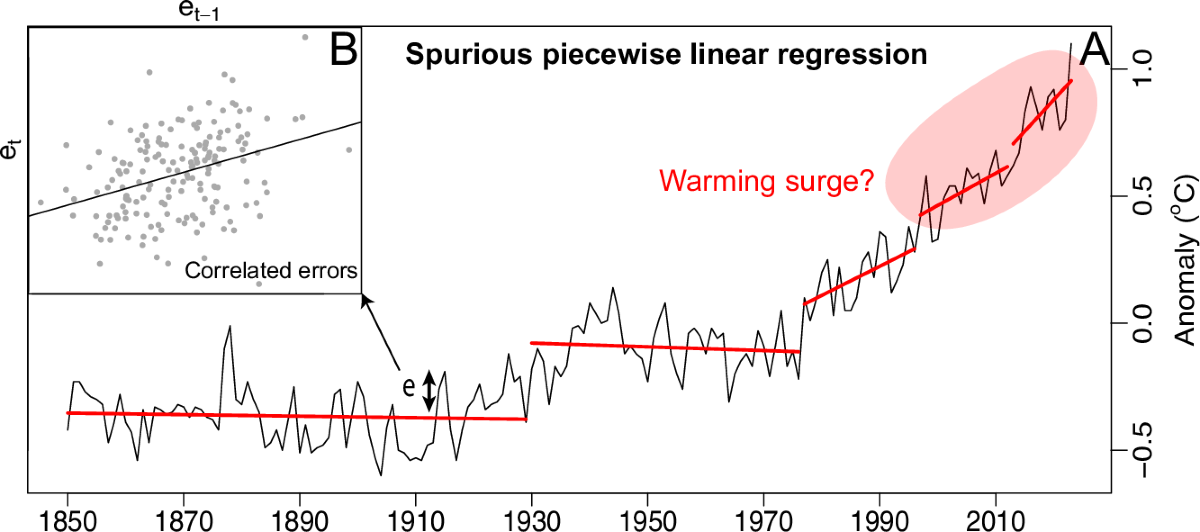
IntroductionGlobal mean surface temperature (GMST) series are essential for tracking global warming. Warming can be quantified by comparing against a baseline period (e.g., pre-industrial levels) or by calculating the rate of change over a defined interval. GMST naturally varies over time, displaying short periods of accelerated or decelerated warming. Significant focus has been directed toward changes in the warming rate within scientific literature and media, particularly regarding recent episodes of accelerated or decelerated warming. Such fluctuations may occur alongside long-term warming and can be influenced by short-term variability or noise in surface temperatures. Here, "trend" refers to the long-term change in mean temperatures, while "noise" encompasses fluctuations around that trend.
Noise in temperature data is typically modeled as a short-memory process, such as autoregression. In these models, oceanic and other slow climate components respond slowly to random atmospheric influences, generating variability over longer time scales than white noise. These short-term fluctuations can obscure long-term warming trends, creating an illusion of slowdown, or may intensify a warming trend, simulating a surge. The crucial question is whether these fluctuations occur independently of any changes in the underlying warming trend, or if there has been a true increase (warming surge) or decrease (warming slowdown) in the trend. Addressing this requires modeling the short-term variability in GMST.
Various studies have suggested that a slowdown in warming (often referred to as a hiatus) took place in the late 1990s, attributing it to multiple factors, including large-scale Pacific Ocean variability and external forcings. However, research focusing on the detection of this warming pause has shown that the rate of change did not decline during this period, and that it was not unusual in light of the existing short-term variability. Specifically, studies utilizing changepoint detection methods—which are designed to identify the timing of trend changes—indicated no significant changes in the warming rate around 1998. Overall, evidence for a pause or slowdown around that time lacks robust statistical support.
According to the Intergovernmental Panel on Climate Change (IPCC), detecting change involves demonstrating that climate or climate-affected systems have changed in a statistically defined manner, without attributing reasons for that change. Typically, attribution requires statistically detecting a change first.
Major climate monitoring agencies rank 2023 as the warmest year recorded since the start of instrumental measurements in 1850. This clearly indicates that global warming has not paused, and current discussions have shifted toward whether a warming acceleration has occurred. Some suggest that the warming rate has increased since 1990 due to a global rise in the Earth's energy imbalance. With lessons learned from the hiatus, this study aims to assess whether a warming surge is statistically detectable.
We utilize changepoint techniques to evaluate the existence of a warming surge since the 1970s and, if present, to estimate its onset. Piecewise linear regression models that allow for trend changes are fitted to GMST datasets and analyzed through changepoint techniques. By not presupposing the timing of any changes—a critical statistical consideration—our analysis prevents overstating significance through selective identification of changepoint locations. We employ both continuous and discontinuous changepoint models to assess the GMST data at an annual scale. Our model fits are evaluated for residual assumptions.Among the various periods analyzed in the literature, the most challenging surge timing to detect is 2015, considering that observations only extend to 2024. This scenario presents only nine years of data following the change. For the trend during this nine-year period to be considered detectable, it would need to be 133% larger (0.044 ∘C/year). As illustrated in Fig. 4, the proximity of a surge to the end of the series complicates its detection. Similar challenges are noted in a simulation study that evaluated detection power for warming increases, taking into account different vantage years and surge timings (see Supplementary Figs. 9–10). Shorter time series (earlier vantage years) and late surges lead to a loss of detection power.
DiscussionGlobal Mean Surface Temperature (GMST) series exhibit temporal fluctuations due to short-term variability, which can create the false impression of surges or slowdowns in warming. While these fluctuations may resemble changes in the warming trend, they often result from random noise within the series. This is particularly relevant in light of discussions regarding the warming hiatus over the past decade and the more recent claims of accelerated warming. Formally detecting surges and pauses requires accounting for noise (or short-term variability) and the uncertainties associated with identifying changepoint times—unless the timing of a changepoint is suggested by independent models, theories, or observations.
In this study, various changepoint models were employed to determine whether an acceleration in warming has occurred since 1970. Different types of changepoint models were tested to assess their sensitivity to model selection. After accounting for short-term variability in GMST (characterized by an autoregressive process), no reliable detection of a warming surge was found after 1970. This conclusion stands whether the changepoint models impose continuity of mean responses between regimes or whether autocorrelation is fixed or time-varying. Furthermore, an acceleration was detected using a discontinuous model that assumes independent errors, which is not a statistically valid modeling choice. It is crucial to assess model fits for overall goodness and to ensure residuals exhibit zero mean and no autocorrelation (white noise). The Supplementary Information provides a detailed analysis of residuals from model fits and tests for residual autocorrelation.
While our analysis focuses on whether there has been a sustained acceleration in global warming, we also note the unusual nature of surface temperature anomalies in 2023. Our model fit (in the continuous mean response model with changing autocorrelation, Fig. 1a) indicates that the 2023 anomaly surpasses the 99th percentile of the expected mean, highlighting a significant deviation from the current warming trend. It may be beneficial to incorporate exogenous variables (such as ENSO) into the model to reduce variability in the residuals, facilitating earlier statistical detection of changes. The absence of detected trend changes in GMST records post-1970 does not exclude the possibility that smaller changes may have occurred; the records might simply be too short, or the changes too subtle, to be identifiable amid short-term variability. Consequently, a simulation study was conducted to evaluate when a warming surge would become detectable in the future. A change in the warming rate of approximately 35% around 2010 is projected to be detectable by circa 2035, applicable for both warming accelerations and slowdowns. Our simulations accommodate either an increase or decrease in trend (two-sided Student’s test). Detection lengths would decrease with one-sided testing (e.g., warming only), but this approach is deemed unjustifiable given recent discussions surrounding a pause in warming. Testing for a warming increase based on the same observations suggesting an increase could exaggerate significance. Ultimately, our finding that an acceleration is not yet detectable at the global level may not hold true at regional levels, suggesting that rigorous detection of regional warming surges should be a priority in future research.
Our conclusions rely on piecewise linear models, which offer a solid first-order approximation of any nonlinearities and help prevent overfitting the data. However, no model can perfectly encapsulate our scenario. The assumption that global surface temperatures exhibit first-order autocorrelation describes year-to-year noise dependency, characterized by short memory and geometric decay over time. Other models used to analyze noise in surface temperature observations include long-memory models (where the decay follows a power law). However, we do not consider these models here, as identifying long-memory necessitates extensive time series, and its effects tend to be more pronounced in sea surface temperatures. Stochastic trend models, where the GMST trend is cointegrated with radiative forcing trends, have also been evaluated, but these models are mainly utilized for detection and attribution studies, while our focus is on detecting changes in the warming trend.
MethodDataThis study analyzes four GMST time series:
Hadley Centre/Climatic Research Unit, Version 5 (HadCRUT): This series, covering annual anomalies from 1850-2023, is available at HadCRUT5 and is relative to the 1961–1990 period.
NOAA Merged Land-Ocean Surface Temperature Analysis (NOAAGlobalTemp v5.1.0): This series, covering annual anomalies from 1850-2023, can be found at NOAA and is based on the 1901–2000 period.
Berkeley Earth Surface Temperatures: Available at Berkeley Earth, this series computes anomalies from the 1961–1990 baseline and spans from 1850–2023.
Goddard Institute for Space Studies (GISS) Surface Temperature Analysis (GISTEMP): This series, covering 1880-2023, can be accessed at GISTEMP and is scaled to the 1951–1980 period.
Changepoint ModelsOur research involves fitting several changepoint time series models that segment the GMST into regimes with similar trends, utilizing piecewise linear regression models. The primary focus is on changes in the trend of the series.
Changepoint analyses divide the data into segments at specified changepoint times. Mathematically, our model allows for m changepoints within the data record t∈{1,…,N}, occurring at times τ1,…,τm, adhering to the order 0=τ0<τ1<τ2<…<τm<N=τm+1. The segment index r(t) assigns a value of 1 for t∈{1,…,τ1}, 2 for t∈{τ1+1,…,τ2}, and so on, resulting in m+1 distinct segments. The model for the entire series is given by:
E[Xt]=f(t,τ1,…,τm)
The regression functions considered include a continuous model that ensures process means meet at the changepoint times, as well as a discontinuous model. The model errors {ϵt} exhibit zero mean and allow for autocorrelation, as discussed further below.
The trend model regression structure follows a simple piecewise linear form:
E[Xt]=αr(t)+βr(t)t
where βr(t) and αr(t) denote the trend slope and intercept, respectively, during regime r(t).
If continuity of the regression response E[Xt] is imposed at the changepoint times, the restrictions lead to a model with m changepoints and m+2 free regression parameters. Expressing the model in terms of the free parameters α1,β1,…,βm+1 results in:
E[Xt]=r=1∑m+1αrI(t∈[τr−1,τr])+r=1∑mβrI(t∈[τr−1,τr])t
The model errors follow a zero-mean autocorrelated time series. In a first-order autoregression (AR(1)), this process adheres to the difference equation:
ϵt=ϕϵt−1+Zt
where {Zt} represents independent and identically distributed Gaussian noise with mean E[Zt]≡0 and variance Var[Zt]≡σ2, with ϕ∈(−1,1) being the autocorrelation parameter that captures the correlation between consecutive errors. It is crucial to account for autocorrelation in climate changepoint analyses, as neglecting it may lead to overestimating the number of changepoints. Higher-order autoregressions can be included if a first-order approach proves inadequate. We will also explore scenarios where the autoregressive parameter varies at each changepoint time, linking ϕ to time


















0 Comments